2022-09-19 Blasius#

Last time#

  • NLsolve Newton solver library

    • p-Laplacian robustness

    • diagnostics

  • Algorithmic differentiation via Zygote

  • Symbolic differentiation

Today#

  • Structured by-hand differentiation

  • Concept of PDE-based inference (inverse problems)

  • The Blasius problem (activity)

using Plots
default(linewidth=3)
using LinearAlgebra
using SparseArrays
using Zygote

function vander(x, k=nothing)
    if k === nothing
        k = length(x)
    end
    V = ones(length(x), k)
    for j = 2:k
        V[:, j] = V[:, j-1] .* x
    end
    V
end

vander (generic function with 2 methods)

Hand coding derivatives: it’s all chain rule and associativity#

\[ df = f'(x) dx \]
function f(x)
    y = x
    for _ in 1:2
        a = y^pi
        b = cos(a)
        c = log(y)
        y = b * c
    end
    y
end

f(1.9), gradient(f, 1.9)

(-1.5346823414986814, (-34.03241959914049,))

function df(x, dx)
    y = x
    dy = dx
    for _ in 1:2
        a = y^pi
        da = pi * y^(pi-1) * dy
        b = cos(a)
        db = -sin(a) * da
        c = log(y)
        dc = 1/y * dy
        y = b * c
        dy = db * c + b * dc
    end
    dy
end

df(1.9, 1)

-34.03241959914048

We can go the other way#

We can differentiate a composition \(h(g(f(x)))\) as

(16)#\[\begin{align} \operatorname{d} h &= h' \operatorname{d} g \\ \operatorname{d} g &= g' \operatorname{d} f \\ \operatorname{d} f &= f' \operatorname{d} x. \end{align}\]

What we’ve done above is called “forward mode”, and amounts to placing the parentheses in the chain rule like

\[ \operatorname d h = \frac{dh}{dg} \left(\frac{dg}{df} \left(\frac{df}{dx} \operatorname d x \right) \right) .\]

The expression means the same thing if we rearrange the parentheses,

\[ \operatorname d h = \left( \left( \left( \frac{dh}{dg} \right) \frac{dg}{df} \right) \frac{df}{dx} \right) \operatorname d x \]

which we can compute with in reverse order via

\[ \underbrace{\bar x}_{\frac{dh}{dx}} = \underbrace{\bar g \frac{dg}{df}}_{\bar f} \frac{df}{dx} .\]

A reverse mode example#

\[ \underbrace{\bar x}_{\frac{dh}{dx}} = \underbrace{\bar g \frac{dg}{df}}_{\bar f} \frac{df}{dx} .\]
function g(x)
    a = x^pi
    b = cos(a)
    c = log(x)
    y = b * c
    y
end
(g(1.4), gradient(g, 1.4))

(-0.32484122107701546, (-1.2559761698835525,))

function gback(x, y_)
    a = x^pi
    b = cos(a)
    c = log(x)
    y = b * c
    # backward pass
    c_ = y_ * b 
    b_ = c * y_
    a_ = -sin(a) * b_
    x_ = 1/x * c_ + pi * x^(pi-1) * a_
    x_
end
gback(1.4, 1)

-1.2559761698835525

Kinds of algorithmic differentation#

  • Source transformation: Fortran code in, Fortran code out

    • Duplicates compiler features, usually incomplete language coverage

    • Produces efficient code

  • Operator overloading: C++ types

    • Hard to vectorize

    • Loops are effectively unrolled/inefficient

  • Just-in-time compilation: tightly coupled with compiler

    • JIT lag

    • Needs dynamic language features (JAX) or tight integration with compiler (Zygote, Enzyme)

    • Some sharp bits

How does Zygote work?#

h1(x) = x^3 + 3*x
h2(x) = ((x * x)  + 3) * x
@code_llvm h1(4.)

;  @ In[7]:1 within `h1`
define double @julia_h1_5414(double %0) #0 {
top:
; ┌ @ intfuncs.jl:322 within `literal_pow`
; │┌ @ operators.jl:591 within `*` @ float.jl:385
    %1 = fmul double %0, %0
    %2 = fmul double %1, %0
; └└
; ┌ @ promotion.jl:389 within `*` @ float.jl:385
   %3 = fmul double %0, 3.000000e+00
; └
; ┌ @ float.jl:383 within `+`
   %4 = fadd double %3, %2
; └
  ret double %4
}

@code_llvm gradient(h1, 4.)

;  @ /home/jed/.julia/packages/Zygote/xGkZ5/src/compiler/interface.jl:95 within `gradient`
define [1 x double] @julia_gradient_5495(double %0) #0 {
top:
;  @ /home/jed/.julia/packages/Zygote/xGkZ5/src/compiler/interface.jl:97 within `gradient`
; ┌ @ /home/jed/.julia/packages/Zygote/xGkZ5/src/compiler/interface.jl:45 within `#60`
; │┌ @ In[7]:1 within `Pullback`
; ││┌ @ /home/jed/.julia/packages/Zygote/xGkZ5/src/compiler/chainrules.jl:206 within `ZBack`
; │││┌ @ /home/jed/.julia/packages/Zygote/xGkZ5/src/lib/number.jl:12 within `literal_pow_pullback`
; ││││┌ @ intfuncs.jl:321 within `literal_pow`
; │││││┌ @ float.jl:385 within `*`
        %1 = fmul double %0, %0
; ││││└└
; ││││┌ @ promotion.jl:389 within `*` @ float.jl:385
       %2 = fmul double %1, 3.000000e+00
; │└└└└
; │┌ @ /home/jed/.julia/packages/Zygote/xGkZ5/src/lib/lib.jl:17 within `accum`
; ││┌ @ float.jl:383 within `+`
     %3 = fadd double %2, 3.000000e+00
; └└└
;  @ /home/jed/.julia/packages/Zygote/xGkZ5/src/compiler/interface.jl:98 within `gradient`
  %.fca.0.insert = insertvalue [1 x double] zeroinitializer, double %3, 0
  ret [1 x double] %.fca.0.insert
}

Forward or reverse?#

It all depends on the shape.

\[ \operatorname d h = \frac{dh}{dg} \left(\frac{dg}{df} \left(\frac{df}{dx} \operatorname d x \right) \right) .\]
\[ \operatorname d h = \left( \left( \left( \frac{dh}{dg} \right) \frac{dg}{df} \right) \frac{df}{dx} \right) \operatorname d x \]

  • One input, many outputs: use forward mode

    • “One input” can be looking in one direction

  • Many inputs, one output: use reverse mode

    • Will need to traverse execution backwards (“tape”)

    • Hierarchical checkpointing

  • About square? Forward is usually a bit more efficient.

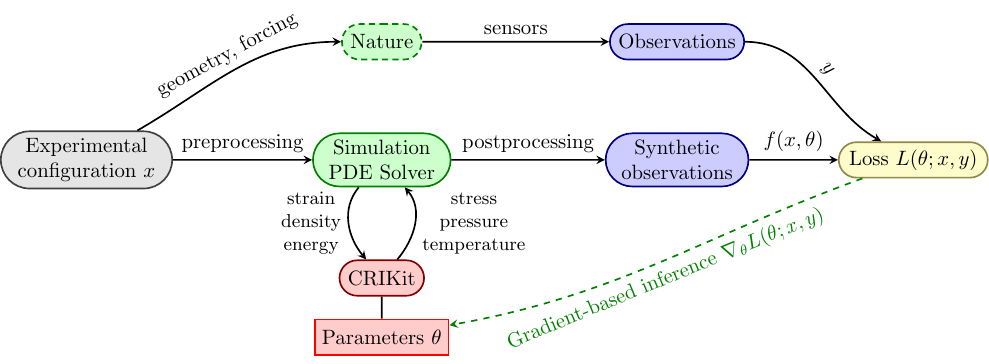
Inference using PDE-based models#

Compressible Blasius boundary layer#

  • Activity will solve this 1D nonlinear PDE