2021-08-23 First Day¶

CSCI-5636: Numerical solution of partial differential equations (PDE)¶

Instructor: Jed Brown, jed.brown@colorado.edu, ECOT 824¶

Meeting: Mon, Wed, Fri at 1:30-12:20 in ECEE 283 (and virtually)¶

What are PDE?¶

partial derivatives¶

Gradient \(\mathbf g(\mathbf x) = \nabla u(\mathbf x)\)
- scalar field to vector field
Curl \(\mathbf c(\mathbf x) = \nabla\times \mathbf g(\mathbf x)\)
vector field to vector field
Divergence \(d(\mathbf x) = \nabla\cdot \mathbf c(\mathbf x)\)
- vector field to scalar field
time derivatives: \(\frac{\partial u(t, \mathbf x)}{\partial t}\)

what do they describe?¶

heat transfer
electrostatics, electromagnetics
solid mechanics
fluid mechanics
quantum mechanics
population dynamics

Find \(u\) such that

(1)¶\[\begin{align} -\nabla\cdot\big(\kappa(\mathbf x) \nabla u(\mathbf x)\big) &= f(\mathbf x) & \mathbf x &\in \Omega \\ u(\mathbf x) &= g(\mathbf x) & \mathbf x &\in \Gamma_D \subset \partial\Omega \\ \kappa(\mathbf x) \nabla u(\mathbf x) \cdot \mathbf{\hat n}(\mathbf x) &= h(\mathbf x) & \mathbf x &\in \Gamma_N \subset\partial\Omega \end{align}\]

What does it mean to discretize a PDE?¶

Find \(u\) such that

(2)¶\[\begin{align} -\nabla\cdot\big(\kappa(\mathbf x) \nabla u(\mathbf x)\big) &= f(\mathbf x) & \mathbf x &\in \Omega \\ u(\mathbf x) &= g(\mathbf x) & \mathbf x &\in \Gamma_D \subset \partial\Omega \\ \nabla u(\mathbf x) \cdot \mathbf{\hat n}(\mathbf x) &= h(\mathbf x) & \mathbf x &\in \Gamma_N \subset\partial\Omega \end{align}\]

How is it satisfied?¶

At grid points with rules to approximate derivatives
- Finite Difference / collocation
A weak (integral) over elements with rules to reconstruct from element averages and define fluxes
- Finite Volume
A weak form over with solution and “test functions” in the same space
- Finite Element / Galerkin

How expensive is it?¶

Suppose our domain is \(\Omega = (0, 1)^3\)

using Plots

# a common "good" discretiation
error(h) = min(1, 10*h^2)

function cost(h)
    n = 1/h # number of points per dimension
    N = n^3 # total number of grid points in 3D
    N
end

function cost2(h)
    N = cost(h)
    N * log2(1 + N)
end

cost2 (generic function with 1 method)

plot([cost, cost2], error, .01, 1, xscale=:log10, yscale=:log10)

../_images/2021-08-23-first-day_9_0.svg

What goes in? What comes out?¶

Equations
- Conservation
- Variational principles
- Materials
Geometry
- meshing needed?
Boundary conditions
- essential/Dirichlet
- natural/Neumann
- mixed
Initial conditions

Discrete solutions
- Sampled on a grid
- Time series
Quantities of Interest (QoI)
- Heat flux
- Maximum temperature
- Maximum stress
- Lift, drag
Eigensolutions
- Resonant frequencies/modes
- Orbitals

Who works with PDE solvers?¶

Numerical analysts
Domain scientists and engineers
Materials scientists
HPC specialists
Optimizers
Statisticians

What skills should they have?¶

Breakout groups: pick one role and make a list of essential and nice-to-have skills, plus at least one question. Pick one member to report out.

…

…

Computer Science = Runnable Abstraction Science¶

In the “grinder”¶

Mathematical language and principles for each major class of method
- What is covered by theory
- When you’re venturing off-trail
- Analytic tools to predict and debug
Realistic cost and exploitable structure
- Performance on modern hardware
- Algebraic solvers and time integrators
Write/modify stand-alone code
Select and use (parallel) libraries

How can you trust the solution?¶

Verification: solving the problem right
Validation: solving the right problem

Abstractions/collaboration¶

Domain scientists, engineers
Optimizers, statisticians
Abstractions that reduce cognitive load
Metrics/visualization for decisions

On programming languages¶

C¶

Reliable and popular for libraries (PETSc, etc.). “Simple”, unsafe, capable of encapsulation.

C++¶

Popular with applications and some libraries. Powerful, but complicated and unsafe.

Fortran¶

The OG of numerical computing. Good for “array programming”, but encapsulation is hard. Unsafe depending on dialect.

Julia¶

For ground-up examples in class and in activities. Capable of high performance, expressive multiple dispatch, works well in a notebook. Library ecosystem for PDEs is limited, but rapidly improving.

Python¶

Good access to JIT, libraries like FEniCS. Poor native performance, but good libraries to compiled code.

Rust¶

New compiled language. Good performance, encapsulation, safety, static analysis. Poor libraries (so far).

You don’t need to know any of these well and you can choose the language for your project.

I won’t grade and I won’t waste your time¶

I will provide feedback

I will be a mentor and guide navigating this field

I will help you get what you want out of the class (with a dash of wholesome context)

My mom said, “basically, your professor is asking you to be an adult”. That was too flexible.

In other classes, I didn’t feel like I could bounce back, but in this one I did.

What about the letter grade?¶

Collect a portfolio of the work and insights you’re most proud of
Individual meetings during the last week of the semester (mid-term preview)
We’ll have a conversation and you’ll propose a grade based on your portfolio
- I’ll trust you.

I can nudge upward when students are too modest – pretty common. In rare cases, I may adjust down.

What I need from you: Growth Mindset¶

How will the semester look?¶

Lecture periods¶

Refresh, introduce, activity/group discussion, reflect
Pointers to further resources/activities

In-class and homework activities¶

(Short) coding, experiments, presentation of results
Use the math and programming tools of the field
Open-ended, go further occasionally

Learning plans¶

Write, track, and revise a personal learning plan.
Meet/chat approx weekly to check in with partner

Projects (second half of semester)¶

Dig into community software for solving PDEs
Short presentation on how the community works
Key stakeholders
Strengths and weaknesses
Discuss and critique

Community contribution¶

Tutorial, documentation, performance study, comparison, new features, new application
Reflect in a short presentation

Tools¶

Git and GitHub¶

GitHub CLassroom to manage repositories
Write using notebooks and markdown
Review using GitHub tools and nbgrader

Zulip¶

math- and code-aware team chat
live, informal
thread managemnet so a question in class can spin off into a deeper asynchronous conversation

Jupyter¶

RISE slides available on website
Activities with scaffolding
Nbgrader for writing feedback
Works with many languages; we’ll mostly use Julia
Collaborative mode (new)

JupyterHub: coding.csel.io ¶

Nothing to install, persistent storage

A note about COVID¶

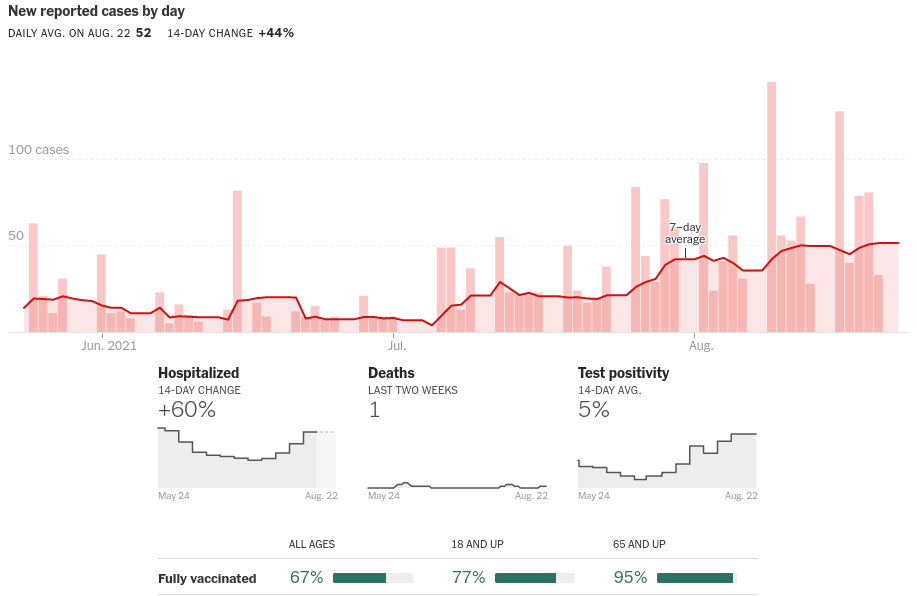
Boulder County cases are high and increasing
Vaccinated can transmit
I have a 1yo and 4yo in childcare
They need to be tested at any symptoms
- 1-2 days to result

I’d prefer to do virtual office hours until 7-day average new cases drops below 20/day
I’ll likely be home with a kid and need to teach remotely or otherwise make it up to you

previous

Slides

next

2021-08-25 Finite Difference Intro