2022-11-14 Ratel Hands-on#

Last time#

  • Intro to solid mechanics, Ratel

  • Singularities and \(hp\) adaptivity

  • Cost of sparse matrices

  • GPU performance with Ratel and context

Today#

  • Solver diagnostics

  • Reading profiles

  • Amortizing costs

Running on Alpine#

$ ssh login.rc.colorado.edu
rc$ module load slurm/alpine
rc$ acompile
acompile$ . /projects/jeka2967/activate.bash

$ git clone \
    https://gitlab.com/micromorph/ratel
$ cd ratel/examples
$ mpiexec -n 1 ratel-quasistatic \
    -options_file FILE.yml

Running in Docker#

Clone the Ratel repository and cd into it

host$ docker run -it --rm -v $(pwd):/work registry.gitlab.com/micromorph/ratel
$ mpiexec -n 2 ratel-quasistatic -options_file ex02-quasistatic-elasticity-multi-material.yml

Suggested test problem#

$ mpiexec -n 6 ratel-quasistatic -options_file ex02-quasistatic-elasticity-schwarz-pendulum.yml

Quasi-Newton methods (BFGS)#

BFGS is a method that does not require a linear solve.

  • It starts with an operation \(J_0^{-1}\), which is meant to be an approximation of the inverse Jacobian (like a preconditioner).

  • Each iteration creates a symmetric rank-2 update,

    \[J_{k+1}^{-1} = \left(I - \frac{s_k z_k^T}{s_k^T z_k}\right) J_k^{-1} \left(I - \frac{s_k z_k^T}{s_k^T z_k}\right) + \frac{s_k s_k^T}{s_k^T z_k}\]

  • BFGS is equivalent to conjugate gradients for a linear problem.

  • -snes_type qn -snes_qn_scale_type jacobian

    • This uses an iterative solve for \(J_0\)

  • Add -ksp_type preonly (skip the iterative solve)

Newton#

  • Good diagnostics because we can tighten linear solve independent from nonlinear.

  • -ksp_converged_reason -ksp_view_singularvalues

  • Are we “over-solving”; see -snes_ksp_ew to automatically adjust during convergence

Quasi-Newton#

  • Fewer Jacobian assemblies and preconditioner setups

  • Maybe fewer linear solve iterations (automatically avoids over-solving)

Solids: efficient matrix-free Jacobians#

cf. Davydov et al. (2020)#

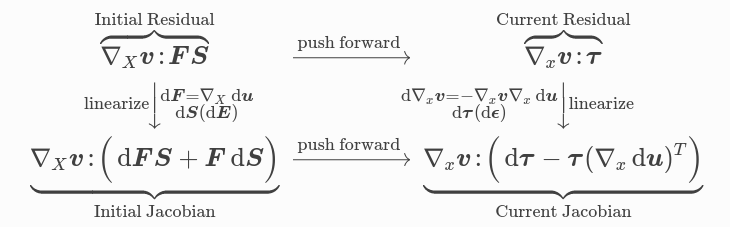
Suggestions (use -ts_view and -log_view)#

  • Change from initial to current configuration

$ git grep model: examples/*.yml

  • Try assembling and using AMG directly (instead of p-MG first): -multigrid amg_only

    • And try a direct solve: -pc_type cholesky

    • Try using one-level domain decomposition -pc_type bjacobi or asm

    • What is the marginal cost of p-refinement (-order) versus h-refinement (see tps refine and layers)?

    • Relative benefit of quasi-Newton?

  • How does thickness affect solve cost? What about Poisson ratio nu? (Edit the input file or override from command line.)

  • Visualization (if you have Paraview)

    • -ts_monitor_solution cgns:sol.cgns (just stores displacement at each time step)

    • -ts_monitor_diagnostic_quantities cgns:diag.cgns (lots of diagnostic fields)

    • -view_diagnostic_quantities vtk:diagnostic.vtu (only at the final time)

    • For CGNS: load Point Arrays (lower left sidebar) and Apply after opening file.

    • “Warp by Vector” (Control-Space to search by name, or use Filters->Common menu)

    • von Mises stress is an indicator for plastic yield (elasticity no longer valid)