Contents

2021-12-01 Finite Volume methods

Last time

  • Notes on unstructured meshing workflow

  • Finite volume methods for hyperbolic conservation laws

  • Riemann solvers for scalar equations

    • Shocks and the Rankine-Hugoniot condition

    • Rarefactions and entropy solutions

Today

  • Higher order methods

  • Godunov’s Theorem

  • Slope reconstruction

  • Slope limiting

using LinearAlgebra
using Plots
default(linewidth=4)

struct RKTable
    A::Matrix
    b::Vector
    c::Vector
    function RKTable(A, b)
        s = length(b)
        A = reshape(A, s, s)
        c = vec(sum(A, dims=2))
        new(A, b, c)
    end
end

rk4 = RKTable([0 0 0 0; .5 0 0 0; 0 .5 0 0; 0 0 1 0], [1, 2, 2, 1] / 6)

function ode_rk_explicit(f, u0; tfinal=1., h=0.1, table=rk4)
    u = copy(u0)
    t = 0.
    n, s = length(u), length(table.c)
    fY = zeros(n, s)
    thist = [t]
    uhist = [u0]
    while t < tfinal
        tnext = min(t+h, tfinal)
        h = tnext - t
        for i in 1:s
            ti = t + h * table.c[i]
            Yi = u + h * sum(fY[:,1:i-1] * table.A[i,1:i-1], dims=2)
            fY[:,i] = f(ti, Yi)
        end
        u += h * fY * table.b
        t = tnext
        push!(thist, t)
        push!(uhist, u)
    end
    thist, hcat(uhist...)
end

function testfunc(x)
    max(1 - 4*abs.(x+2/3),
        abs.(x) .< .2,
        (2*abs.(x-2/3) .< .5) * cospi(2*(x-2/3)).^2
    )
end

riemann_advection(uL, uR) = 1*uL # velocity is +1

function fv_solve1(riemann, u_init, n, tfinal=1)
    h = 2 / n
    x = LinRange(-1+h/2, 1-h/2, n) # cell midpoints (centroids)
    idxL = 1 .+ (n-1:2*n-2) .% n
    idxR = 1 .+ (n+1:2*n) .% n
    function rhs(t, u)
        fluxL = riemann(u[idxL], u)
        fluxR = riemann(u, u[idxR])
        (fluxL - fluxR) / h
    end
    thist, uhist = ode_rk_explicit(
        rhs, u_init.(x), h=h, tfinal=tfinal)
    x, thist, uhist
end

function riemann_burgers(uL, uR)
    flux = zero(uL)
    for i in 1:length(flux)
        fL = flux_burgers(uL[i])
        fR = flux_burgers(uR[i])
        flux[i] = if uL[i] > uR[i] # shock
            max(fL, fR)
        elseif uL[i] > 0 # rarefaction all to the right
            fL
        elseif uR[i] < 0 # rarefaction all to the left
            fR
        else
            0
        end
    end
    flux
end

function riemann_traffic(uL, uR)
    flux = zero(uL)
    for i in 1:length(flux)
        fL = flux_traffic(uL[i])
        fR = flux_traffic(uR[i])
        flux[i] = if uL[i] < uR[i] # shock
            min(fL, fR)
        elseif uL[i] < .5 # rarefaction all to the right
            fL
        elseif uR[i] > .5 # rarefaction all to the left
            fR
        else
            flux_traffic(.5)
        end
    end
    flux
end

riemann_traffic (generic function with 1 method)

Godunov’s Theorem (1954)

Linear numerical methods

\[ \dot u_i = \sum_j a_{ij} u_j \]
for solving time-dependent PDE can be at most first order accurate if they are monotone.

For our purposes, monotonicity is equivalent to positivity preservation,

\[ \min_x u(0, x) \ge 0 \quad \Longrightarrow \quad \min_x u(t, 0) \ge 0 .\]

Discontinuities

A numerical method for representing a discontinuous function on a stationary grid can be no better than first order accurate in the \(L^1\) norm,

\[ \lVert u - u^* \rVert_{L^1} = \int \lvert u - u^* \rvert . \]
If we merely sample a discontinuous function, say
\[\begin{split} u(x) = \begin{cases} 0, & x \le a \\ 1, & x > a \end{cases} \end{split}\]
onto a grid with element size \(\Delta x\) then we will have errors of order 1 on an interval proportional to \(\Delta x\).

In light of these two observations, we may still ask for numerical methods that are more than first order accurate for smooth solutions, but those methods must be nonlinear.

Slope Reconstruction

One method for constructing higher order methods is to use the state in neighboring elements to perform a conservative reconstruction of a piecewise polynomial, then compute numerical fluxes by solving Riemann problems at the interfaces. If \(x_i\) is the center of cell \(i\) and \(g_i\) is the reconstructed gradient inside cell \(i\), our reconstructed solution is

\[ \tilde u_i(x) = u_i + g_i \cdot (x - x_i) . \]
We would like this reconstruction to be monotone in the sense that
\[ \Big(\tilde u_i(x) - \tilde u_j(x) \Big) \Big( u_i - u_j \Big) \ge 0 \]
for any \(x\) on the interface between element \(i\) and element \(j\).

Question

Is the symmetric slope

\[ \hat g_i = \frac{u_{i+1} - u_{i-1}}{2 \Delta x} \]
monotone?

Slope limiting

We will determine gradients by “limiting” the above slope using a nonlinear function that reduces to 1 when the solution is smooth. There are many ways to express limiters and our discussion here roughly follows Berger, Aftosmis, and Murman (2005).

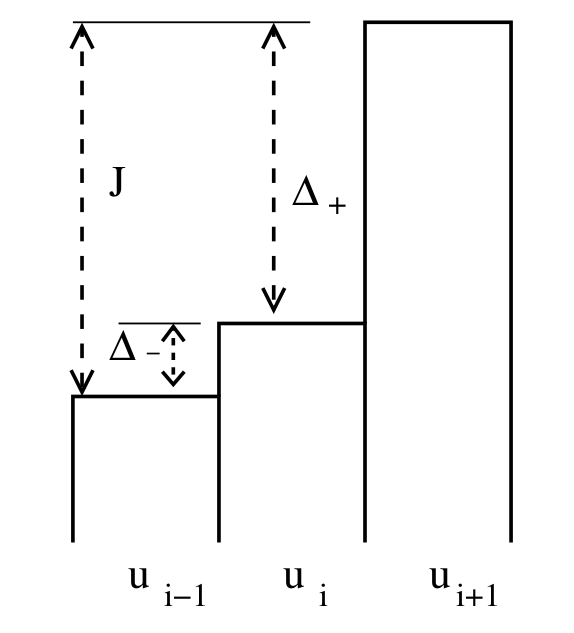
Berger et al, figure 3b, Cell averages

We will express a slope limiter in terms of the ratio

\[ r_i = \frac{u_i - u_{i-1}}{u_{i+1} - u_{i-1}} \]
and use as a gradient,
\[ g_i = \phi(r_i) \frac{u_{i+1} - u_{i-1}}{2 \Delta x} . \]
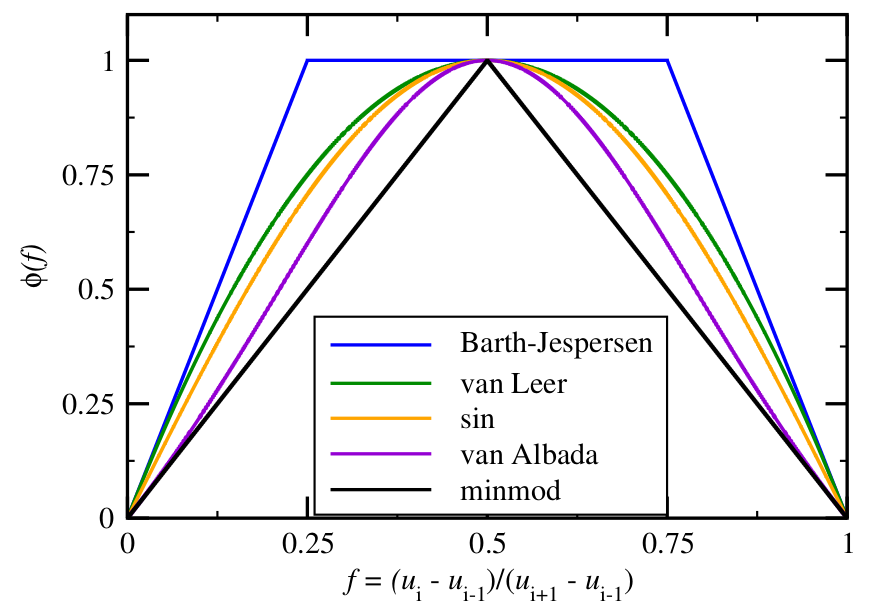Our functions \(\phi\) will be zero unless \(0 < r < 1\) and \(\phi(1/2) = 1\). Berger et al, figure 3a, Symmetric form of slope limiters All of these limiters are second order accurate and TVD; those that fall below minmod are not second order accurate and those that are above Barth-Jesperson are not second order accurate, not TVD, or produce artifacts.

Common limiters

limit_zero(r) = 0
limit_none(r) = 1
limit_minmod(r) = max(min(2*r, 2*(1-r)), 0)
limit_sin(r) = (0 < r && r < 1) * sinpi(r)
limit_vl(r) = max(4*r*(1-r), 0)
limit_bj(r) = max(0, min(1, 4*r, 4*(1-r)))
limiters = [limit_zero limit_none limit_minmod limit_sin limit_vl limit_bj];

plot(limiters, label=limiters, xlims=(-.1, 1.1))
../_images/2021-12-01-slope-reconstruction_14_0.svg

A slope-limited solver

function fv_solve2(riemann, u_init, n, tfinal=1, limit=limit_sin)
    h = 2 / n
    x = LinRange(-1+h/2, 1-h/2, n) # cell midpoints (centroids)
    idxL = 1 .+ (n-1:2*n-2) .% n
    idxR = 1 .+ (n+1:2*n) .% n
    function rhs(t, u)
        jump = u[idxR] - u[idxL]
        r = (u - u[idxL]) ./ jump
        r[isnan.(r)] .= 0
        g = limit.(r) .* jump / 2h
        fluxL = riemann(u[idxL] + g[idxL]*h/2, u - g*h/2)
        fluxR = fluxL[idxR]
        (fluxL - fluxR) / h
    end
    thist, uhist = ode_rk_explicit(
        rhs, u_init.(x), h=h, tfinal=tfinal)
    x, thist, uhist
end

fv_solve2 (generic function with 3 methods)

x, thist, uhist = fv_solve2(riemann_advection, testfunc, 100, .5,
    limit_sin)
plot(x, uhist[:,1:10:end], legend=:none)
../_images/2021-12-01-slope-reconstruction_17_0.svg