2022-11-16 FE for Compressible flow#

Last time#

  • Solver diagnostics

  • Reading profiles

  • Amortizing costs

Today#

  • Equations

    • Conservation

    • Choice of variables

  • SUPG stabilization

  • Solvers

  • Boundary conditions

using Plots
default(linewidth=3)
using LinearAlgebra
using SparseArrays

Conservation of mass, momentum, and energy#

\[\frac{\partial \bm{q}}{\partial t} + \nabla \cdot \bm{F}(\bm{q}) -S(\bm{q}) = 0\]
\[\begin{split}\bm{q} = \begin{pmatrix} \rho \\ \rho \bm{ u }\\ E \equiv \rho e \end{pmatrix} \begin{array}{l} \leftarrow\textrm{ volume mass density}\\ \leftarrow\textrm{ momentum density}\\ \leftarrow\textrm{ energy density} \end{array}\end{split}\]

  • Equation of state

(59)#\[\begin{align} P &= \Big(\underbrace{\frac{c_p}{c_v}}_{\gamma} - 1\Big)\underbrace{\left(E - \frac\rho 2 \bm u \cdot \bm u - \rho g z \right)}_{\rho e_{\text{internal}}} \\ T &= e_{\text{internal}} / c_v \end{align}\]

\begin{aligned} \bm{F}(\bm{q}) &= \underbrace{\begin{pmatrix} \rho\bm{u}\ {\rho \bm{u} \otimes \bm{u}} + P \bm{I}3 \ {(E + P)\bm{u}} \end{pmatrix}}{\bm F_{\text{adv}}} + \underbrace{\begin{pmatrix} 0 \

  • \bm{\sigma} \

  • \bm{u} \cdot \bm{\sigma} - k \nabla T \end{pmatrix}}{\bm F{\text{diff}}},\ S(\bm{q}) &=

  • (60)#\[\begin{pmatrix} 0\\ \rho g \bm{\hat{k}}\\ 0 \end{pmatrix}\]

\end{aligned}

Choice of variables#

Acoustic wave speed#

\[a = \sqrt{c_p(\gamma - 1) T}\]

material

speed

air

340 m/s

water

1500 m/s

Mach number#

\[\mathrm{Ma} = \frac{\lVert \bm u \rVert}{a}\]

Primitive variables#

\[\begin{split}\bm y = \begin{pmatrix} P \\ \bm u \\ T \end{pmatrix}\end{split}\]

Using the equation of state, we can write \(\bm y(\bm q)\) or \(\bm q(\bm y)\). But these transformations are ill conditioned for \(\mathrm{Ma} \ll 1\).

\[ \frac{\partial \bm q}{\partial t} = \frac{\partial \bm q}{\partial \bm y} \frac{\partial \bm y}{\partial t}\]

Blasius profile (thanks, Leila Ghaffari)#

  • Take an analytic Blasius profile.

  • Primitive: Write \(\bm y\) in a piecewise linear space with nodally exact values.

  • Conservative: Write \(\bm q\) in a piecewise linear space with nodally exact values.

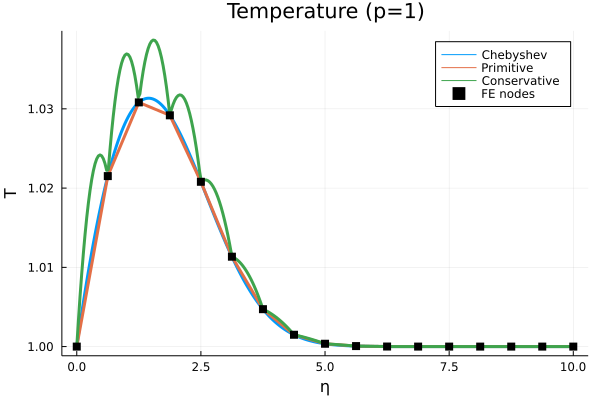
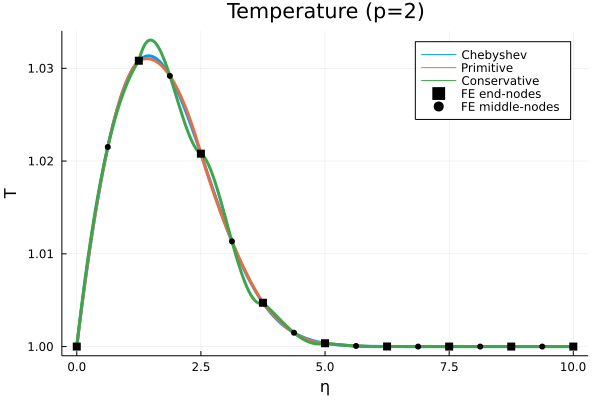
Stabilization#

(61)#\[\begin{align} \int_{\Omega} \bm v \cdot \left( \frac{\partial \bm{q}}{\partial t} - \bm{S}(\bm{y}) \right) \,dV - \int_{\Omega} \nabla \bm v \!:\! \bm{F}(\bm{y})\,dV & \\ + \int_{\partial \Omega} \bm v \cdot \bm{F}(\bm{y}) \cdot \widehat{\bm{n}} \,dS & \\ + \int_{\Omega} \nabla \bm v : \frac{\partial \bm F_{\text{adv}}}{\partial \bm q} \bm \tau \left( \frac{\partial \bm{q}}{\partial t} \, + \, \nabla \cdot \bm{F} \, (\bm{y}) - \bm{S}(\bm{y}) \right) \,dV &= 0 \end{align}\]

Time integration#

  • Fully implicit \(G(t, \bm y, \dot{\bm y}) = 0\) with generalized alpha.

  • Newton method, usually about 3 iterations per time step.

  • Krylov method

    • GMRES when using a strong preconditioner

      • Block Jacobi/incomplete LU

    • BCGS(\(\ell\)) with a weak preconditioner

      • Point-block Jacobi

Running on Alpine#

$ ssh login.rc.colorado.edu
rc$ module load slurm/alpine
rc$ acompile
acompile$ . /projects/jeka2967/activate.bash

$ git clone \
    https://github.com/CEED/libCEED
$ cd libCEED/examples/fluids
$ make
$ mpiexec -n 1 ./navierstokes \
    -options_file FILE.yaml

Running in Docker#

Clone the libCEED repository and cd libCEED/examples/fluids

host$ docker run -it --rm -v $(pwd):/work registry.gitlab.com/micromorph/ratel
$ make
$ mpiexec -n 2 ./navierstokes -options_file FILE.yaml