2023-10-06 2D Advection-diffusion and waves#

Last time#

  • Implicit Runge-Kutta methods

  • Exploring/discussing tradeoffs

  • SciML benchmarks suite (DifferentialEquations.jl)

Today#

  • FD methods in 2D

  • Cost profile

  • The need for fast algebraic solvers

  • Wave equation and Hamiltonians

  • Symplectic integrators

using Plots
default(linewidth=3)
using LinearAlgebra
using SparseArrays

function my_spy(A)
    cmax = norm(vec(A), Inf)
    s = max(1, ceil(120 / size(A, 1)))
    spy(A, marker=(:square, s), c=:diverging_rainbow_bgymr_45_85_c67_n256, clims=(-cmax, cmax))
end
    
function plot_stability(Rz, title; xlims=(-2, 2), ylims=(-2, 2))
    x = LinRange(xlims[1], xlims[2], 100)
    y = LinRange(ylims[1], ylims[2], 100)
    heatmap(x, y, (x, y) -> abs(Rz(x + 1im*y)), c=:bwr, clims=(0, 2), aspect_ratio=:equal, title=title)
end

struct RKTable
    A::Matrix
    b::Vector
    c::Vector
    function RKTable(A, b)
        s = length(b)
        A = reshape(A, s, s)
        c = vec(sum(A, dims=2))
        new(A, b, c)
    end
end

function rk_stability(z, rk)
    s = length(rk.b)
    1 + z * rk.b' * ((I - z*rk.A) \ ones(s))
end

rk4 = RKTable([0 0 0 0; .5 0 0 0; 0 .5 0 0; 0 0 1 0], [1, 2, 2, 1] / 6)

function ode_rk_explicit(f, u0; tfinal=1., h=0.1, table=rk4)
    u = copy(u0)
    t = 0.
    n, s = length(u), length(table.c)
    fY = zeros(n, s)
    thist = [t]
    uhist = [u0]
    while t < tfinal
        tnext = min(t+h, tfinal)
        h = tnext - t
        for i in 1:s
            ti = t + h * table.c[i]
            Yi = u + h * sum(fY[:,1:i-1] * table.A[i,1:i-1], dims=2)
            fY[:,i] = f(ti, Yi)
        end
        u += h * fY * table.b
        t = tnext
        push!(thist, t)
        push!(uhist, u)
    end
    thist, hcat(uhist...)
end

ode_rk_explicit (generic function with 1 method)

Extending advection-diffusion to 2D#

1 dimension#

(20)#\[\begin{align} u_t + (- \kappa u_x + w u)_x &= f(x) & \text{ on } \Omega &= (a,b) \\ u(a) &= g_D(a) & u'(b) &= g_N(b) \end{align}\]

  • Cell Peclet number \(\mathrm{Pe}_h = \frac{\lvert w \rvert h}{\kappa}\)

    • \(\mathrm{Pe}_h \lesssim 1\) avoids oscillations

    • \(\mathrm{Pe}_h \gtrsim 1\) is non-stiff for time-dependent model

  • Centered versus upwind for advection

  • Need uniformly bounded \(\kappa \ge \epsilon > 0\)

  • “Strong form” not defined at discontinuities in \(\kappa\)

    • Works okay using divergence form and fluxes at staggered points

2 dimensions#

(21)#\[\begin{align} u_t + \nabla\cdot\big(- \kappa \nabla u + \mathbf{w} u \big) &= f(x,y) & \text{ on } \Omega & \subset \mathbb R^2 \\ u|_{\Gamma_D} &= g_D(x,y) \\ (-\kappa \nabla u + \mathbf w u) \cdot \hat n|_{\Gamma_N} &= g_N(x,y) \end{align}\]

  • \(\Omega\) is some well-connected open set (we will assume simply connected) and the Dirichlet boundary \(\Gamma_D \subset \partial \Omega\) is nonempty.

  • Finite difference methods don’t have an elegant/flexible way to specify boundaries

  • We’ll choose \(\Omega = (-1, 1) \times (-1, 1)\)

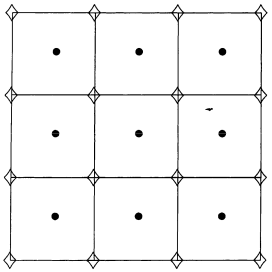
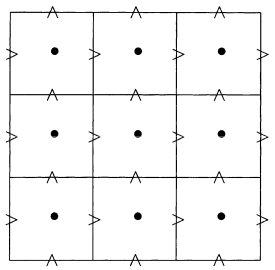
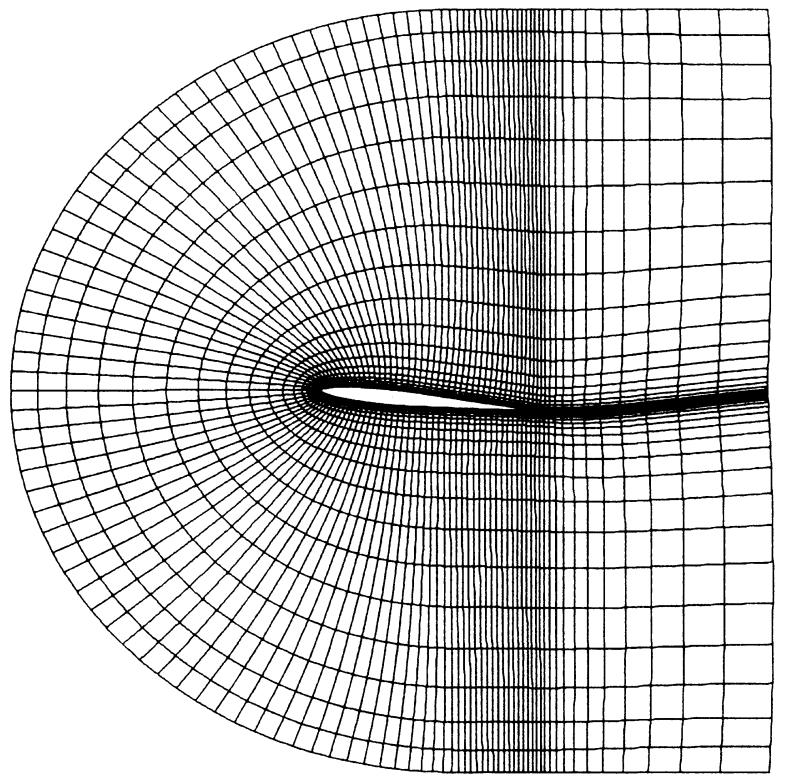
On finite difference grids#

  • Non-uniform grids can mesh “special” domains

    • Rare in 3D; overset grids, immersed boundary methods

  • Concept of staggering is complicated/ambiguous

Wesseling 11.4: A boundary-fitted grid around an airfoil.

Time-independent advection-diffusion#

Advection#

\[ \nabla\cdot(\mathbf w u) = \mathbf w \cdot \nabla u + (\nabla\cdot \mathbf w) u\]

If we choose divergence-free \(\mathbf w\), we can use the stencil

\[\begin{split} \mathbf w \cdot \nabla u \approx \frac 1 h \begin{bmatrix} & w_2 & \\ -w_1 & & w_1 \\ & -w_2 & \end{bmatrix} \!:\! \begin{bmatrix} u_{i-1, j+1} & u_{i, j+1} & u_{i+1,j+1} \\ u_{i-1, j} & u_{i, j} & u_{i+1,j} \\ u_{i-1, j-1} & u_{i, j-1} & u_{i+1,j-1} \\ \end{bmatrix} \end{split}\]

Diffusion#

\[ -\nabla\cdot(\kappa \nabla u) = -\kappa \nabla\cdot \nabla u - \nabla\kappa\cdot \nabla u\]

  • When would you trust this decomposition?

  • If we have constant \(\kappa\), we can write

    \[\begin{split} -\kappa \nabla\cdot \nabla u \approx \frac{\kappa}{h^2} \begin{bmatrix} & -1 & \\ -1 & 4 & -1 \\ & -1 & \end{bmatrix} \!:\! \begin{bmatrix} u_{i-1, j+1} & u_{i, j+1} & u_{i+1,j+1} \\ u_{i-1, j} & u_{i, j} & u_{i+1,j} \\ u_{i-1, j-1} & u_{i, j-1} & u_{i+1,j-1} \\ \end{bmatrix} \end{split}\]

Advection-diffusion in code#

function advdiff_matrix(n; kappa=1, wind=[1, 1]/sqrt(2))
    h = 2 / n
    rows = Vector{Int64}()
    cols = Vector{Int64}()
    vals = Vector{Float64}()
    idx(i, j) = (i-1)*n + j
    stencil_advect = [-wind[1], -wind[2], 0, wind[1], wind[2]] / h
    stencil_diffuse = [-1, -1, 4, -1, -1] * kappa / h^2
    for i in 1:n
        for j in 1:n
            if i in [1, n] || j in [1, n]
                push!(rows, idx(i, j))
                push!(cols, idx(i, j))
                push!(vals, 1.)
            else
                append!(rows, repeat([idx(i,j)], 5))
                append!(cols, [idx(i-1,j), idx(i,j-1), idx(i,j), idx(i+1,j), idx(i,j+1)])
                append!(vals, stencil_advect + stencil_diffuse)
            end
        end
    end
    sparse(rows, cols, vals)
end

advdiff_matrix (generic function with 1 method)

Spy the matrix#

A = advdiff_matrix(6, wind=[1, 0], kappa=.001)
my_spy(A)

A = advdiff_matrix(20, wind=[2, 1], kappa=.01)
ev = eigvals(Matrix(-A))
scatter(real(ev), imag(ev))
scatter!([0], [0], color=:black, label=:none, marker=:plus)

Plot a solution#

n = 50
x = LinRange(-1, 1, n)
y = x
f = cos.(pi*x/2) * cos.(pi*y/2)'
heatmap(x, y, f, aspect_ratio=:equal)

A = advdiff_matrix(n, wind=[2,1], kappa=.01)
u = A \ vec(f)
heatmap(x, y, reshape(u, n, n), aspect_ratio=:equal)

  • What happens when advection dominates?

  • As you refine the grid?

Cost breadown and optimization#

using ProfileSVG
function assemble_and_solve(n)
    A = advdiff_matrix(n)
    x = LinRange(-1, 1, n)
    f = cos.(pi*x/2) * cos.(pi*x/2)'
    u = A \ vec(f)
end

@profview assemble_and_solve(400)

[ Info: Precompiling ProfileSVG [132c30aa-f267-4189-9183-c8a63c7e05e6]
WARNING: using AbstractTrees.isroot in module LeftChildRightSiblingTrees conflicts with an existing identifier.
ERROR: LoadError: UndefVarError: `parentlinks` not defined
Stacktrace:
 [1] getproperty(x::Module, f::Symbol)
   @ Base ./Base.jl:31
 [2] top-level scope
   @ ~/.julia/packages/LeftChildRightSiblingTrees/FaxpE/src/abstracttrees.jl:10
 [3] include(mod::Module, _path::String)
   @ Base ./Base.jl:457
 [4] include(x::String)
   @ LeftChildRightSiblingTrees ~/.julia/packages/LeftChildRightSiblingTrees/FaxpE/src/LeftChildRightSiblingTrees.jl:1
 [5] top-level scope
   @ ~/.julia/packages/LeftChildRightSiblingTrees/FaxpE/src/LeftChildRightSiblingTrees.jl:248
 [6] include
   @ ./Base.jl:457 [inlined]
 [7] include_package_for_output(pkg::Base.PkgId, input::String, depot_path::Vector{String}, dl_load_path::Vector{String}, load_path::Vector{String}, concrete_deps::Vector{Pair{Base.PkgId, UInt128}}, source::String)
   @ Base ./loading.jl:2049
 [8] top-level scope
   @ stdin:3
in expression starting at /home/jed/.julia/packages/LeftChildRightSiblingTrees/FaxpE/src/abstracttrees.jl:10
in expression starting at /home/jed/.julia/packages/LeftChildRightSiblingTrees/FaxpE/src/LeftChildRightSiblingTrees.jl:1
in expression starting at stdin:3
ERROR: LoadError: Failed to precompile LeftChildRightSiblingTrees [1d6d02ad-be62-4b6b-8a6d-2f90e265016e] to "/home/jed/.julia/compiled/v1.9/LeftChildRightSiblingTrees/jl_PEarVe".
Stacktrace:
  [1] error(s::String)
    @ Base ./error.jl:35
  [2] compilecache(pkg::Base.PkgId, path::String, internal_stderr::IO, internal_stdout::IO, keep_loaded_modules::Bool)
    @ Base ./loading.jl:2300
  [3] compilecache
    @ ./loading.jl:2167 [inlined]
  [4] _require(pkg::Base.PkgId, env::String)
    @ Base ./loading.jl:1805
  [5] _require_prelocked(uuidkey::Base.PkgId, env::String)
    @ Base ./loading.jl:1660
  [6] macro expansion
    @ ./loading.jl:1648 [inlined]
  [7] macro expansion
    @ ./lock.jl:267 [inlined]
  [8] require(into::Module, mod::Symbol)
    @ Base ./loading.jl:1611
  [9] include
    @ ./Base.jl:457 [inlined]
 [10] include_package_for_output(pkg::Base.PkgId, input::String, depot_path::Vector{String}, dl_load_path::Vector{String}, load_path::Vector{String}, concrete_deps::Vector{Pair{Base.PkgId, UInt128}}, source::String)
    @ Base ./loading.jl:2049
 [11] top-level scope
    @ stdin:3
in expression starting at /home/jed/.julia/packages/FlameGraphs/8Yi2s/src/FlameGraphs.jl:1
in expression starting at stdin:3
ERROR: LoadError: Failed to precompile FlameGraphs [08572546-2f56-4bcf-ba4e-bab62c3a3f89] to "/home/jed/.julia/compiled/v1.9/FlameGraphs/jl_xG79gN".
Stacktrace:
  [1] error(s::String)
    @ Base ./error.jl:35
  [2] compilecache(pkg::Base.PkgId, path::String, internal_stderr::IO, internal_stdout::IO, keep_loaded_modules::Bool)
    @ Base ./loading.jl:2300
  [3] compilecache
    @ ./loading.jl:2167 [inlined]
  [4] _require(pkg::Base.PkgId, env::String)
    @ Base ./loading.jl:1805
  [5] _require_prelocked(uuidkey::Base.PkgId, env::String)
    @ Base ./loading.jl:1660
  [6] macro expansion
    @ ./loading.jl:1648 [inlined]
  [7] macro expansion
    @ ./lock.jl:267 [inlined]
  [8] require(into::Module, mod::Symbol)
    @ Base ./loading.jl:1611
  [9] include
    @ ./Base.jl:457 [inlined]
 [10] include_package_for_output(pkg::Base.PkgId, input::String, depot_path::Vector{String}, dl_load_path::Vector{String}, load_path::Vector{String}, concrete_deps::Vector{Pair{Base.PkgId, UInt128}}, source::Nothing)
    @ Base ./loading.jl:2049
 [11] top-level scope
    @ stdin:3
in expression starting at /home/jed/.julia/packages/ProfileSVG/ecSyU/src/ProfileSVG.jl:1
in expression starting at stdin:3

Failed to precompile ProfileSVG [132c30aa-f267-4189-9183-c8a63c7e05e6] to "/home/jed/.julia/compiled/v1.9/ProfileSVG/jl_70v1YB".

Stacktrace:
 [1] error(s::String)
   @ Base ./error.jl:35
 [2] compilecache(pkg::Base.PkgId, path::String, internal_stderr::IO, internal_stdout::IO, keep_loaded_modules::Bool)
   @ Base ./loading.jl:2300
 [3] compilecache
   @ ./loading.jl:2167 [inlined]
 [4] _require(pkg::Base.PkgId, env::String)
   @ Base ./loading.jl:1805
 [5] _require_prelocked(uuidkey::Base.PkgId, env::String)
   @ Base ./loading.jl:1660
 [6] macro expansion
   @ ./loading.jl:1648 [inlined]
 [7] macro expansion
   @ ./lock.jl:267 [inlined]
 [8] require(into::Module, mod::Symbol)
   @ Base ./loading.jl:1611

What’s left?#

  • Symmetric Dirichlet boundary conditions

  • Symmetric Neumann boundary conditions

  • Verification with method of manufactured solutions

  • Non-uniform grids

  • Upwinding for advection-dominated problems

  • Variable coefficients

  • Time-dependent problems

  • Fast algebraic solvers

Gas equations of state#

There are many ways to describe a gas

Name

variable

units

pressure

\(p\)

force/area

density

\(\rho\)

mass/volume

temperature

\(T\)

Kelvin

(specific) internal energy

\(e\)

energy/mass

entropy

\(s\)

energy/Kelvin

Equation of state#

\[ \rho, e \mapsto p, T \]

Ideal gas#

(22)#\[\begin{align} p &= \rho R T & e &= e(T) \end{align}\]
\[ p = (\gamma - 1) \rho e \]
pressure(rho, T) = rho*T

contour(LinRange(0, 2, 30), LinRange(0, 2, 30), pressure, xlabel="\$\\rho\$", ylabel="\$T\$")

Conservation equations#

Mass#

Let \(\mathbf u\) be the fluid velocity. The mass flux (mass/time) moving through an area \(A\) is

\[ \int_A \rho \mathbf u \cdot \hat{\mathbf n} .\]

If mass is conserved in a volume \(V\) with surface \(A\), then the total mass inside the volume must evolve as

\[ \int_V \rho_t = \left( \int_V \rho \right)_t = - \underbrace{\int_A \rho\mathbf u \cdot \hat{\mathbf n}}_{\int_V \nabla\cdot (\rho\mathbf u)},\]

where we have applied the divergence theorem. Dropping the integrals over arbitrary volumes, we have the evolution equation for conservation of mass.

\[ \rho_t + \nabla\cdot (\rho \mathbf u) = 0 \]

Momentum#

The momentum \(\rho \mathbf u\) has a flux that includes

  • convection \(\rho \mathbf u \otimes \mathbf u\)

    • this is saying that each component of momentum is carried along in the vector velocity field

  • pressure \(p I\)

  • viscous \(-\boldsymbol\tau\)

A similar integral principle leads to the momentum equation

\[ (\rho \mathbf u)_t + \nabla\cdot\big[ \rho \mathbf u \otimes \mathbf u + p I - \boldsymbol \tau \big] = 0 \]