2023-11-13 Ratel for Solid Mechanics

Last time

• Stabilized methods

• Dispersion diagrams

• Mixed finite elements

Today

• Intro to solid mechanics, Ratel

• Singularities and \(hp\) adaptivity

• Cost of sparse matrices

• GPU performance with Ratel and context

using Plots
default(linewidth=3)
using LinearAlgebra
using SparseArrays

Solid mechanics: Ratel Theory Guide

Material coordinates

The current configuration \(x\) is a function of the initial configuration \(X\). We typically solve for displacement \(u = x - X\), and define the deformation gradient

\[ F = \frac{\partial x}{\partial X} = I + \underbrace{\frac{\partial u}{\partial X}}_H\]

where \(H\) is known as displacement gradient.

Conservation

Mass by definition of density

Momentum by equations we solve

Angular momentum by symmetry of stress and strain tensors

Momentum balance in initial configuration

\[\nabla\cdot \mathbf F \mathbf S = 0\]

where \(\mathbf F = I + H\) and \(\mathbf S\) is the symmetric stress tensor (Second Piola-Kirchhoff tensor).

Strain measures

Stress \(\mathbf S\) must be defined as a function of displacement. A common choice is to define the right Cauchy-Green tensor

\[ C = F^T F\]

This has value \(I\) for zero strain. A better formulation uses

\[ E = \frac 1 2 (C - I) = \underbrace{\frac 1 2 (H + H^T + H^T H)}_{\text{stable}}\]

Neo-Hookean model

Strain energy density \begin{aligned} \psi \left(\mathbf{E} \right) &= \frac{\lambda}{2} \left( \log J \right)^2 - \mu \log J + \frac \mu 2 \left( \operatorname{trace} \mathbf{C} - 3 \right) \ &= \frac{\lambda}{2} \left( \log J \right)^2 - \mu \log J + \mu \operatorname{trace} \mathbf{E}, \end{aligned}

\[\mathbf S = \frac{\partial \psi}{\partial \mathbf E}\]

Nonlinear solid mechanics

Industrial models are riddled with singularities

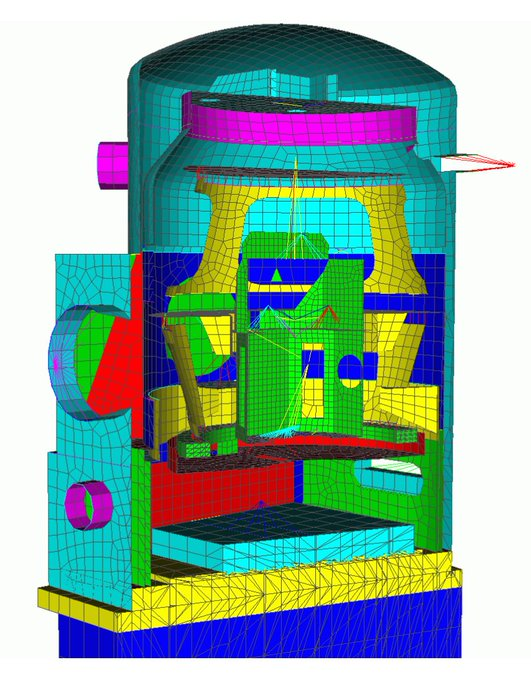
• Every reentrant corner

• Every Dirichlet (fixed/clamped) to Neumann boundary transitien

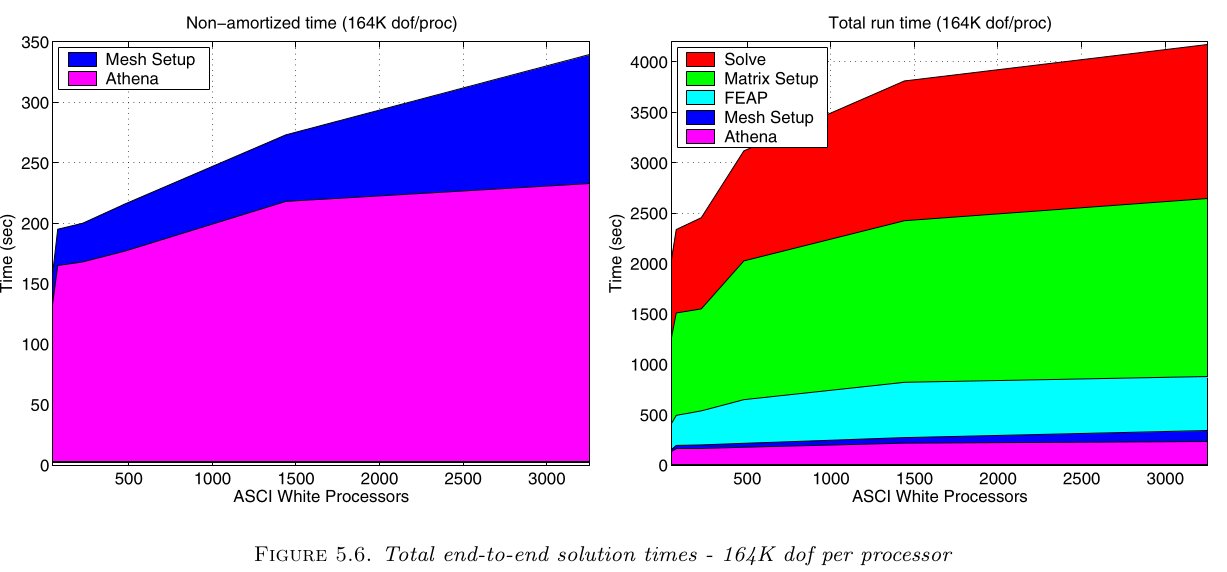
(From Bhardwaj et al, 2002.)

The mathematician’s way: \(hp\) adaptive finite elements

Elliptic PDE always have singularities at reentrant corners (and Dirichlet to Neumann boundary transitions).

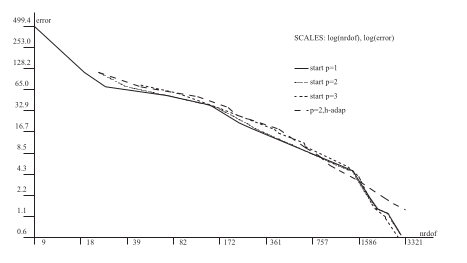
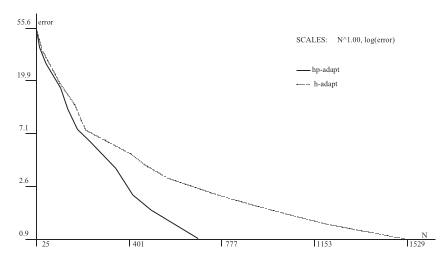
How does it work?

High order to resolve when solution is smooth, tiny low-order elements near singularities.

(source: Deal.II step 27)

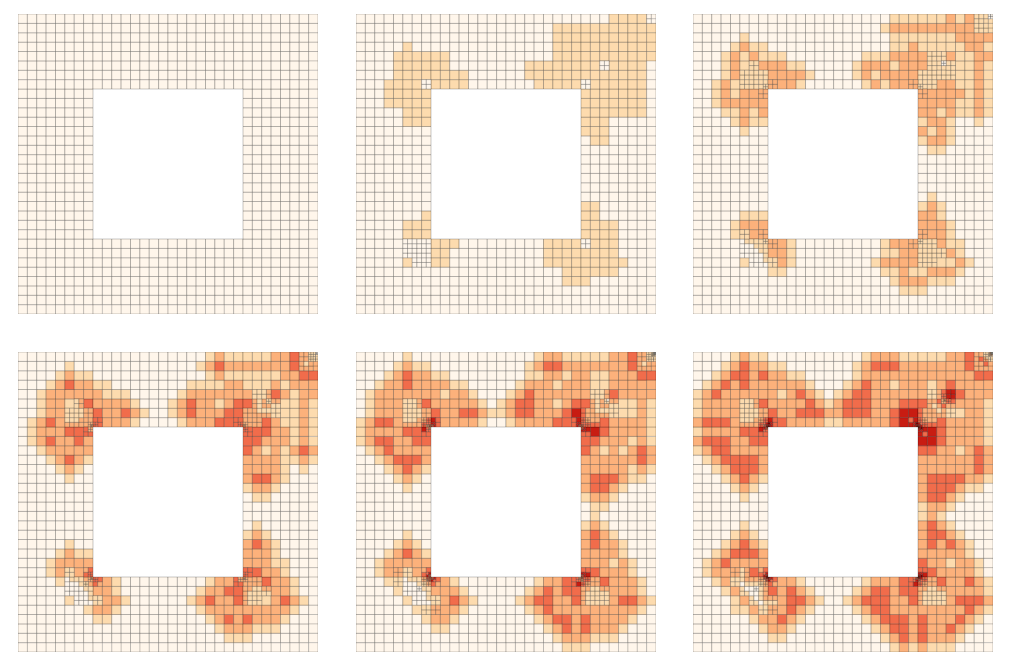
What meshes do engineers use?

source: Ansys blog

Approximation constants are good for high order

Spurious stress singularities

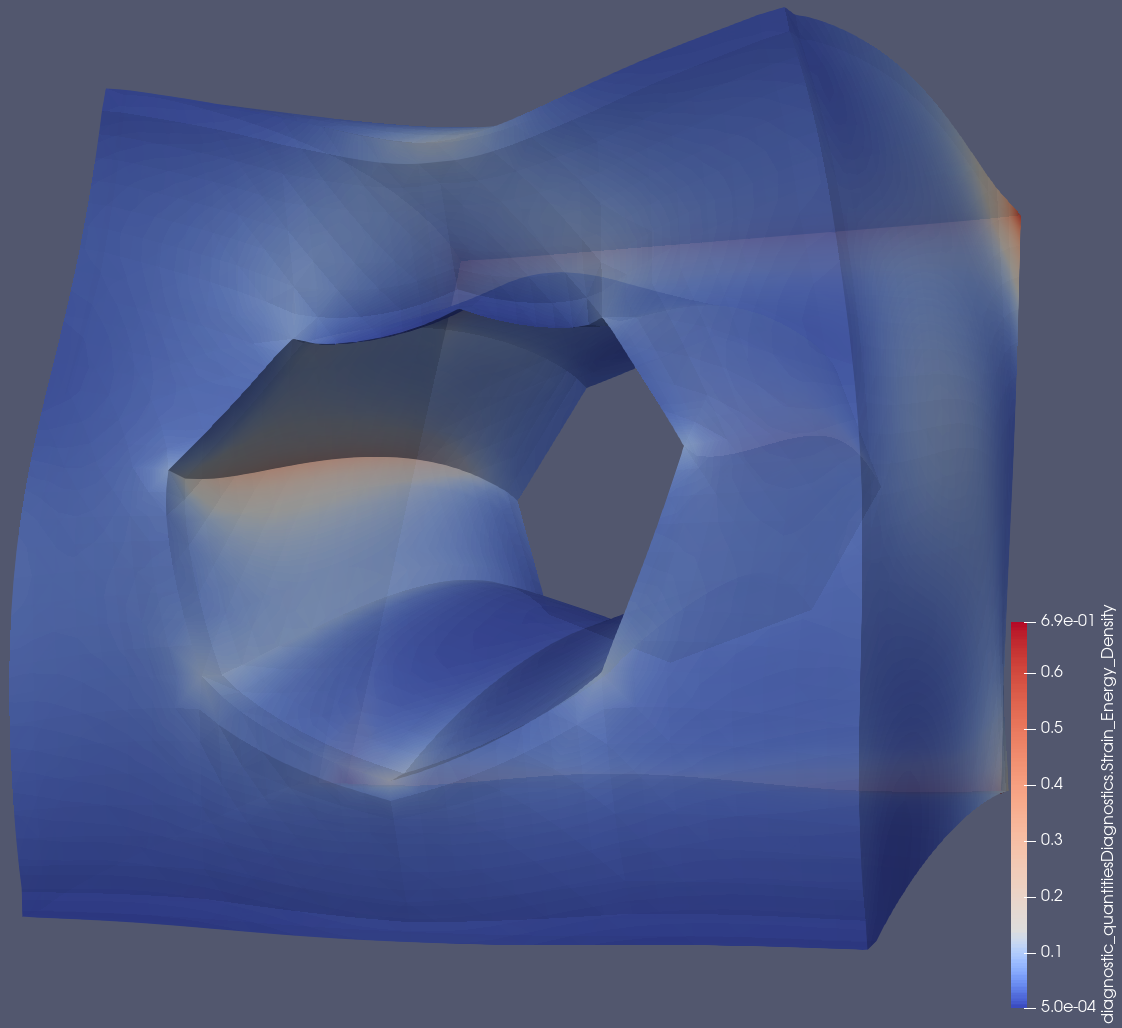
• Geometric model has a round cylinder, no singularity

• Linear meshes have weak reentrant corners

• Moving to quadratic geometry elements is generally good enough

• Gmsh supports arbitrary order

Why matrix-free?

• Assembled matrices need at least 4 bytes transferred per flop. Hardware does 10 flops per byte.

• Matrix-free methods store and move less data, compute faster.

Matrix-free is faster for \(Q_1\) elements

\(p\)-multigrid algorithm and cost breakdown

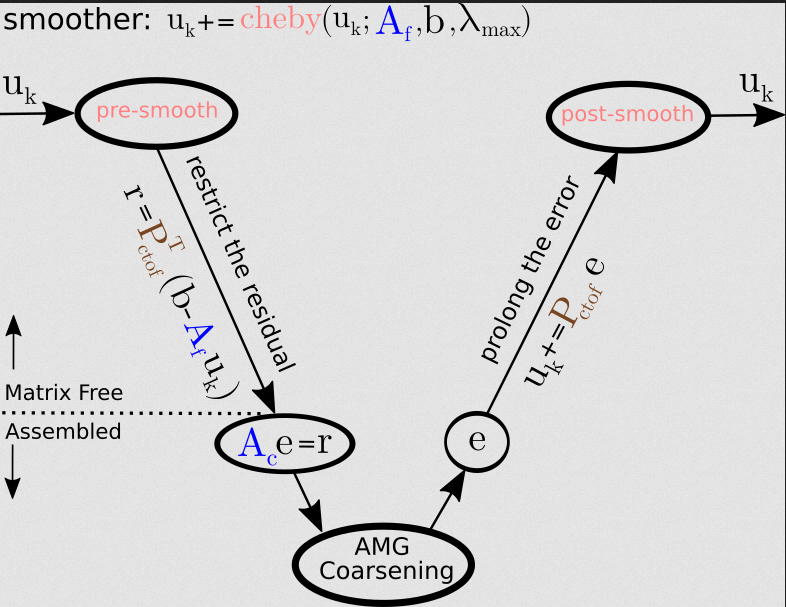
Nonlinear solve efficiency

\(Q_2\) elements

\(Q_3\) elements

Linear solve efficiency

\(Q_2\) elements

\(Q_3\) elements

• Coarse solver is hypre BoomerAMG tuned configured for elasticity; thanks Victor Paludetto Magri.

Preconditioner setup efficiency

\(Q_2\) elements

\(Q_3\) elements

One node of Crusher vs historical Gordon Bell

184 MDoF \(Q_2\) elements nonlinear analysis in seconds

2002 Gordon Bell (Bhardwaj et al)

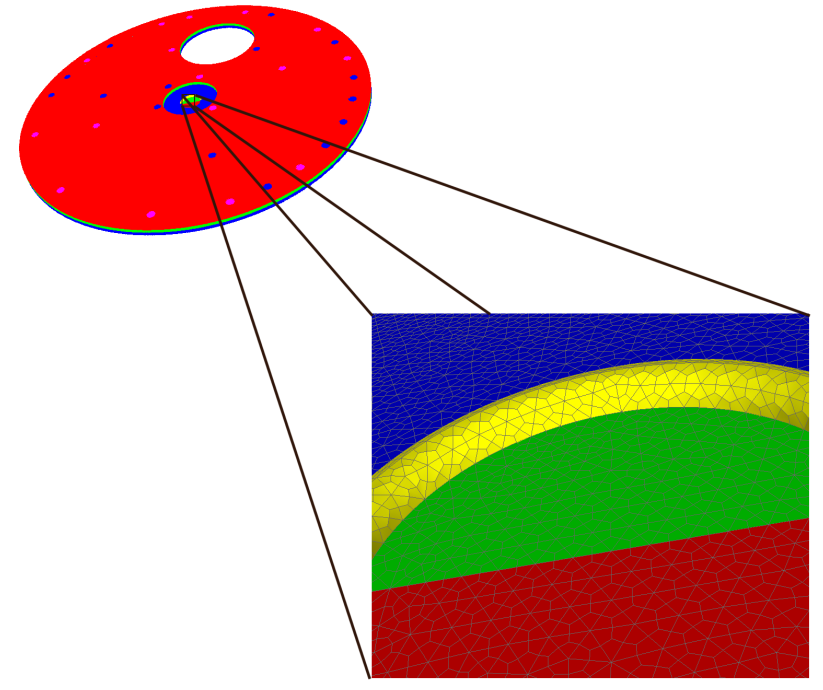
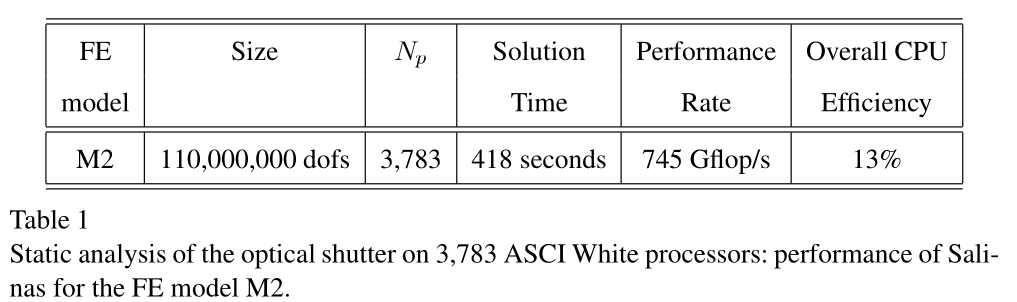
2004 Gordon Bell (Adams et al)

Old performance model

Iterative solvers: Bandwidth

• SpMV arithmetic intensity of 1/6 flop/byte

• Preconditioners also mostly bandwidth

  • Architectural latency a big problem on GPUs, especially for sparse triangular solves.

  • Sparse matrix-matrix products for AMG setup

Direct solvers: Bandwidth and Dense compute

• Leaf work in sparse direct solves

• Dense factorization of supernodes

  • Fundamentally nonscalable, granularity on GPUs is already too big to apply on subdomains

• Research on H-matrix approximations (e.g., in STRUMPACK)

New performance model

Still mostly bandwidth

• Reduce storage needed at quadrature points

  • Half the cost of a sparse matrix already for linear elements

  • Big efficiency gains for high order

• Assembled coarse levels are much smaller.

Compute

• Kernel fusion is necessary

• Balance vectorization with cache/occupancy

• \(O(n)\), but benefits from BLIS-like abstractions | BLIS | libCEED | |——|———| | packing | batched element restriction | | microkernel | basis action | | ? | user-provided qfunctions |

Solids: efficient matrix-free Jacobians

cf. Davydov et al. (2020)

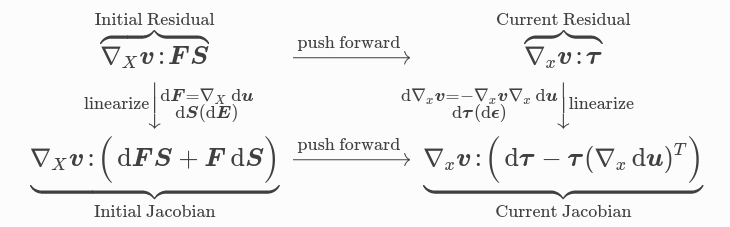
Stable formulations for large-deformation solid mechanics

Solving for \(\mathbf u(\mathbf X)\). Let \(H = \frac{\partial \mathbf u}{\partial \mathbf X}\) (displacement gradient) and \(F = I + H\) (deformation gradient).

Textbook approach

• Stress as a function of \(F\): \(J = \operatorname{det} F\), \(C = F^T F\)

  \[S = \lambda \log J\, C^{-1} + \mu (I - C^{-1})\]

Unstable for small strain, \(F \approx I\) and \(J \approx 1\).

Stable approach

• Stable strain calculation

  \[E = \underbrace{(C - I)/2}_{\text{unstable}} = (H + H^T + H^T H)/2\]

• Compute \(J_{-1} = J - 1\) in a stable way

• Stress

  \[S = \lambda \operatorname{\tt log1p}J_{-1}\, C^{-1} + 2 \mu C^{-1} E\]

This opens the door to dynamic mixed precision algorithms, with computationally intensive physics evaluated using single precision.

Outlook: https://ratel.micromorph.org

• You can move from \(Q_1\) to \(Q_2\) elements for about 2x cost (despite 8x more DoFs)

• Mesh to resolve geometry, \(p\)-refine to pragmatic accuracy

• libCEED isn’t just for high order; already 2x operator apply benefit for \(Q_1\)

• Gordon Bell scale from 20 years ago \(\mapsto\) interactive on a workstation (if you can buy MI250X 😊)

• \(p\)-multigrid, low-memory representation of matrix-free Jacobian

• Multi-node GPU on CUDA and ROCm

• Also good for implicit dynamics