2023-11-06 Solid Mechanics#

Last time#

  • Stabilized methods for transport

    • VMS and SUPG

  • FE interfaces

Today#

  • Mixed finite elements

  • Intro to solid mechanics, Ratel

using Plots
default(linewidth=3)
using LinearAlgebra
using SparseArrays
using FastGaussQuadrature
import NLsolve: nlsolve

function my_spy(A)
    cmax = norm(vec(A), Inf)
    s = max(1, ceil(120 / size(A, 1)))
    spy(A, marker=(:square, s), c=:diverging_rainbow_bgymr_45_85_c67_n256, clims=(-cmax, cmax))
end

function vander_legendre_deriv(x, k=nothing)
    if isnothing(k)
        k = length(x) # Square by default
    end
    m = length(x)
    Q = ones(m, k)
    dQ = zeros(m, k)
    Q[:, 2] = x
    dQ[:, 2] .= 1
    for n in 1:k-2
        Q[:, n+2] = ((2*n + 1) * x .* Q[:, n+1] - n * Q[:, n]) / (n + 1)
        dQ[:, n+2] = (2*n + 1) * Q[:,n+1] + dQ[:,n]
    end
    Q, dQ
end

function febasis(P, Q, quadrature=gausslegendre)
    x, _ = gausslobatto(P)
    q, w = quadrature(Q)
    Pk, _ = vander_legendre_deriv(x)
    Bp, Dp = vander_legendre_deriv(q, P)
    B = Bp / Pk
    D = Dp / Pk
    x, q, w, B, D
end

function fe1_mesh(P, nelem)
    x = LinRange(-1, 1, nelem+1)
    rows = Int[]
    cols = Int[]
    for i in 1:nelem
        append!(rows, (i-1)*P+1:i*P)
        append!(cols, (i-1)*(P-1)+1:i*(P-1)+1)
    end
    x, sparse(cols, rows, ones(nelem*P))'
end

function xnodal(x, P)
    xn = Float64[]
    xref, _ = gausslobatto(P)
    for i in 1:length(x)-1
        xL, xR = x[i:i+1]
        append!(xn, (xL+xR)/2 .+ (xR-xL)/2 * xref[1+(i>1):end])
    end
    xn
end

struct FESpace
    P::Int
    Q::Int
    nelem::Int
    x::Vector
    xn::Vector
    Et::SparseMatrixCSC{Float64, Int64}
    q::Vector
    w::Vector
    B::Matrix
    D::Matrix
    function FESpace(P, Q, nelem, quadrature=gausslegendre)
        x, E = fe1_mesh(P, nelem)
        xn = xnodal(x, P)
        _, q, w, B, D = febasis(P, Q, quadrature)
        new(P, Q, nelem, x, xn, E', q, w, B, D)
    end
end

# Extract out what we need for element e
function fe_element(fe, e)
    xL, xR = fe.x[e:e+1]
    q = (xL+xR)/2 .+ (xR-xL)/2*fe.q
    w = (xR - xL)/2 * fe.w
    E = fe.Et[:, (e-1)*fe.P+1:e*fe.P]'
    dXdx = ones(fe.Q) * 2 / (xR - xL)
    q, w, E, dXdx
end

function fe_residual(u_in, fe, fq; bci=[1], bcv=[1.])
    u = copy(u_in); v = zero(u)
    u[bci] = bcv
    for e in 1:fe.nelem
        q, w, E, dXdx = fe_element(fe, e)
        B, D = fe.B, fe.D
        ue = E * u
        uq = B * ue
        Duq = dXdx .* (D * ue)
        f0, f1 = fq(q, uq, Duq)
        ve = B' * (w .* f0) + D' * (dXdx .* w .* f1)
        v += E' * ve
    end
    v[bci] = u_in[bci] - u[bci]
    #println("residual")
    v
end

function fe_jacobian(u_in, fe, dfq; bci=[1], bcv=[1.])
    u = copy(u_in); u[bci] = bcv
    rows, cols, vals = Int[], Int[], Float64[]
    for e in 1:fe.nelem
        q, w, E, dXdx = fe_element(fe, e)
        B, D, P = fe.B, fe.D, fe.P
        ue = E * u
        uq = B * ue; Duq = dXdx .* (D * ue)
        K = zeros(P, P)
        for j in 1:fe.P
            du = B[:,j]
            Ddu = dXdx .* D[:,j]
            df0, df1 = dfq(q, uq, du, Duq, Ddu)
            K[:,j] = B' * (w .* df0) + D' * (dXdx .* w .* df1)
        end
        inds = rowvals(E')
        append!(rows, kron(ones(P), inds))
        append!(cols, kron(inds, ones(P)))
        append!(vals, vec(K))
    end
    A = sparse(rows, cols, vals)
    A[bci, :] .= 0; A[:, bci] .= 0
    A[bci,bci] = diagm(ones(length(bci)))
    A
end

fe_jacobian (generic function with 1 method)

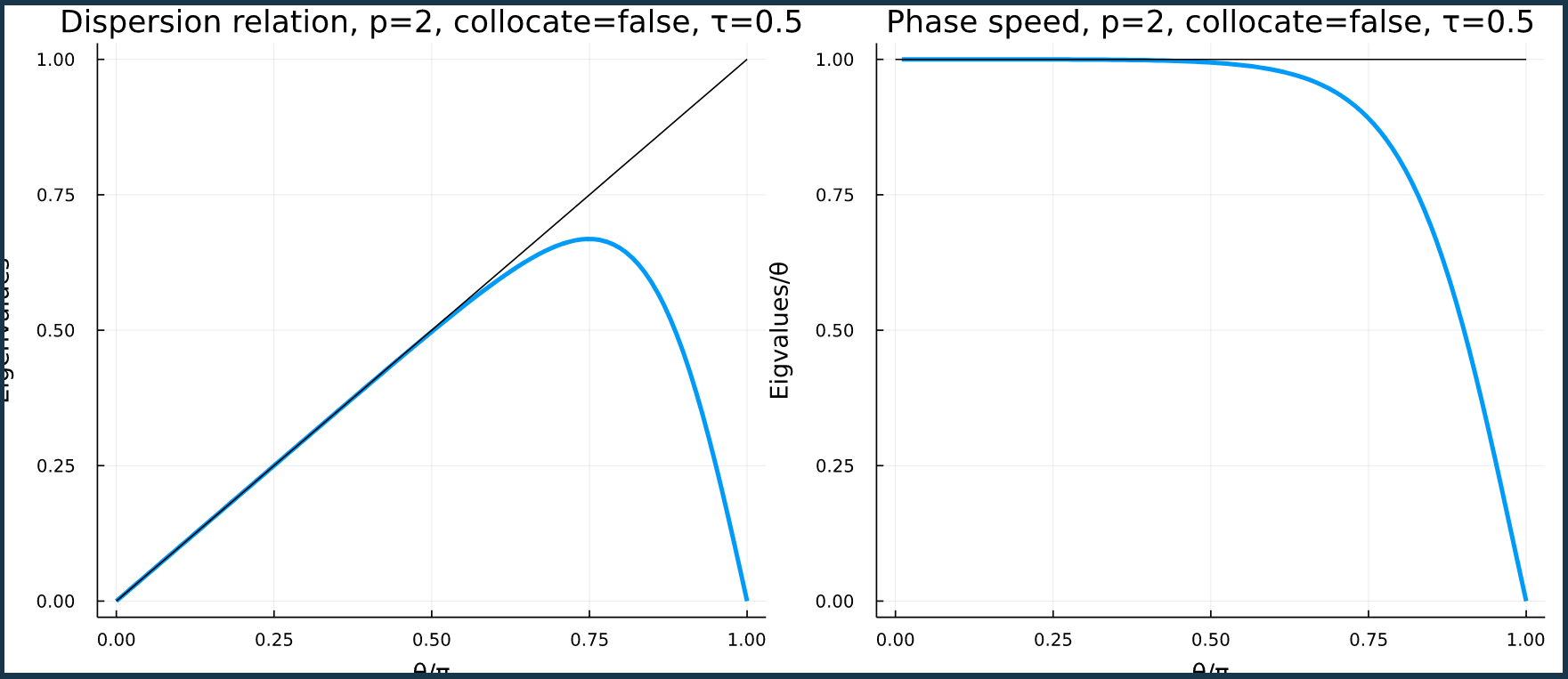
SUPG dispersion diagram (consistent)#

LFAToolkit.jl

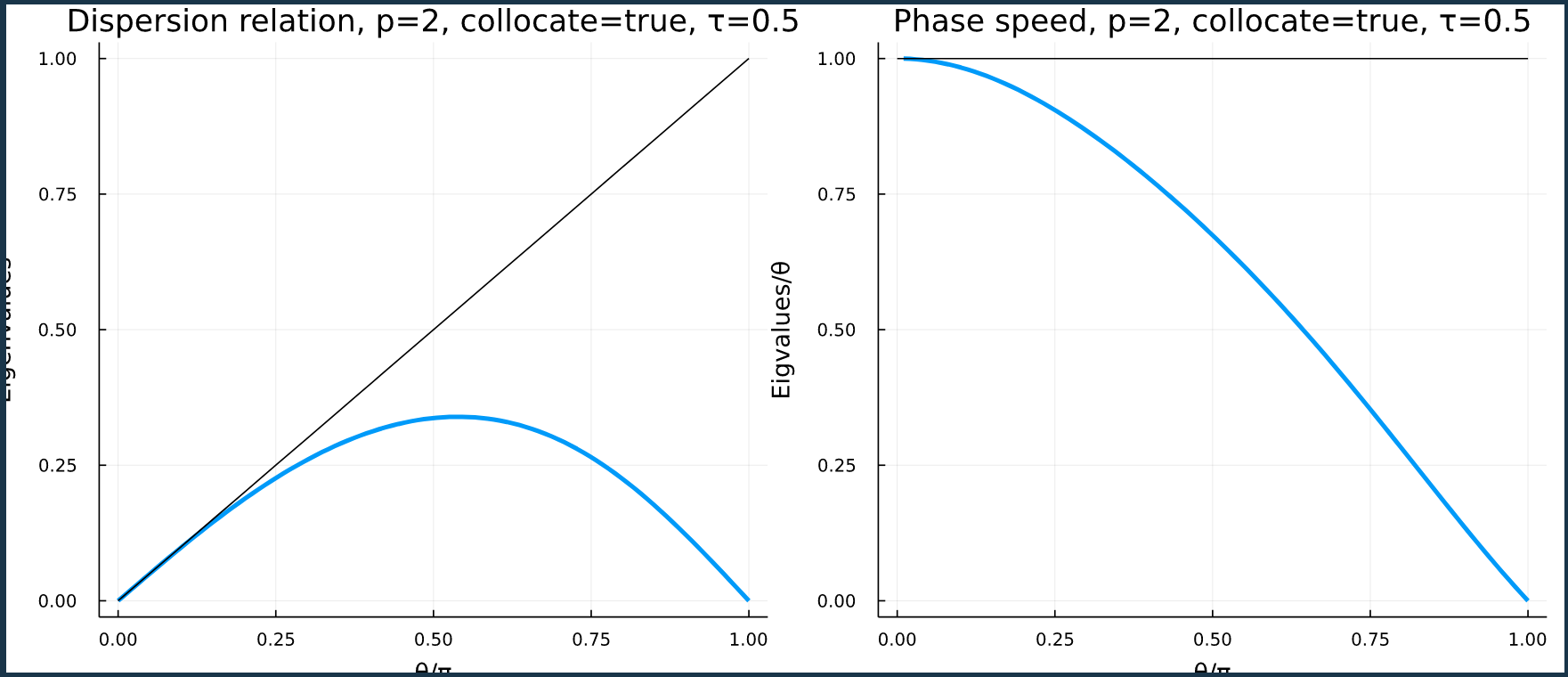
SUPG dispersion diagram (lumped)#

Finite element interfaces: Deal.II#

\[\begin{gather*} v^T F(u) \sim \int_\Omega v \cdot \color{olive}{f_0(u, \nabla u)} + \nabla v \!:\! \color{olive}{f_1(u, \nabla u)} \quad v^T J w \sim \int_\Omega \begin{bmatrix} v \\ \nabla v \end{bmatrix}^T \color{teal}{\begin{bmatrix} f_{0,0} & f_{0,1} \\ f_{1,0} & f_{1,1} \end{bmatrix}} \begin{bmatrix} w \\ \nabla w \end{bmatrix} \\ J w = \sum_e \mathcal E_e^T \underbrace{\begin{bmatrix} B_I \\ B_{\nabla} \end{bmatrix}^T \begin{bmatrix} I & \\ & \left( \frac{\partial X}{\partial x}\right)^T \end{bmatrix}}_{\texttt{fe\_values}} W_q \color{teal}{\begin{bmatrix} f_{0,0} & f_{0,1} \\ f_{1,0} & f_{1,1} \end{bmatrix}} \underbrace{\begin{bmatrix} I & \\ & \left( \frac{\partial X}{\partial x}\right) \end{bmatrix} \begin{bmatrix} B_I \\ B_{\nabla} \end{bmatrix}}_{\texttt{fe\_values}} \mathcal E_e w_L \end{gather*}\]
for e in elems:
    fe_values.reinit()
    for q in q_points:
        for i in test_functions:
            for j in trial_functions
                K_e[i,j] += ...
            f_e[i] += ...
    for f in e.faces:
        if f.at_boundary():
            fe_face_values.reinit()
            for q in q_points:
                ...

Finite element interfaces: MOOSE#

Materials#

  • Can be written without knowledge of finite elements

  • Registration allows libraries of materials (some in MOOSE, others packaged separatle)

  • Example: crystal plasticity

  • Code is C++, so can do dirty things

    • table lookups, proprietary code

    • implicit materials (Newton solve at each quadrature point)

Composition in configuration files#

  • Add fields and coupling

  • Select materials from libraries

  • Multiphysics composition

  • Multiscale coupling

Graphical interface: Peacock#

Periodic table of finite elements#

Careful choice of mixed elements allows exactly satisfying discrete identities#

\[ \nabla\cdot\nabla\times u = 0\]
\[ \nabla\times\nabla u = 0\]

  • Generalized concept: Finite Element Exterior Calculus (FEEC)

  • Improved stability or numerical properties

  • Higher order of accuracy for quantity of interest despite non-smooth problem

\(H^1\) Poisson#

Find \(p\) such that

\[\int \nabla q \cdot \kappa \nabla p = \int q f, \quad \forall q\]

Mixed Poisson#

Find \(\mathbf u, p\) such that

(55)#\[\begin{align} \int \mathbf v \cdot \kappa^{-1} \mathbf u - p \nabla\cdot \mathbf v &= 0 & \forall \mathbf v \\ \int -q \nabla\cdot \mathbf u &= -\int q f & \forall q \end{align}\]

Dirichlet (essential) and Neumann (natural) boundary conditions are swapped, and we get a “saddle point” linear problem $$\begin{pmatrix} M & B^T \ B & 0 \end{pmatrix} \begin{pmatrix} \mathbf u \ p \end{pmatrix} =

(56)#\[\begin{pmatrix} 0 \\ -f \end{pmatrix}\]

$\( With appropriate choice of spaces, \)p,q\( can live in a piecewise constant space while attaining second order accuracy in the fluxes \)\mathbf u$.

Problems with constraints#

Stokes: (slow) incompressible flow#

Find velocity \(\mathbf u\) and pressure \(p\) such that

(57)#\[\begin{align} -\nabla\cdot(\eta \nabla^s \mathbf u - pI) &= 0 \\ \nabla\cdot \mathbf u &= 0 \end{align}\]

where \(\nabla^s \mathbf u\) is the symmetric part of the \(3\times 3\) gradient \(\nabla \mathbf u\).

Weak form: find \((\mathbf u, p)\) such that

\[ \int \nabla^s \mathbf v \!:\! \eta \!:\! \nabla^s \mathbf u - p \nabla\cdot \mathbf v - q \nabla\cdot \mathbf u = 0, \quad \forall (\mathbf v, q)\]

Inf-sup stability#

For this problem to be well posed, it is necessary that the divergence of velocity spans the pressure space “nicely”. This is quantified by the “inf-sup constant” (aka. Ladyzhenskaya–Babuška–Brezzi constant)

\[\beta = \inf_{\lVert p \rVert =1} \sup_{\mathbf u \ne 0} \frac{\int p \nabla\cdot \mathbf u}{\int \nabla^s \mathbf u \!:\! \eta \!:\! \nabla^s \mathbf u}\]

The method loses accuracy if \(\beta\) decays: you want it to stay of order 1 uniformly. Stability can be quantified numerically by solving an eigenvalue problem (1993). This short paper has many figures quantifying stable and unstable elements.

Solid mechanics: Ratel Theory Guide#

Material coordinates#

The current configuration \(x\) is a function of the initial configuration \(X\). We typically solve for displacement \(u = x - X\), and define the deformation gradient

\[ F = \frac{\partial x}{\partial X} = I + \underbrace{\frac{\partial u}{\partial X}}_H\]
where \(H\) is known as displacement gradient.

Conservation#

Mass by definition of density#

Momentum by equations we solve#

Angular momentum by symmetry of stress and strain tensors#

Momentum balance in initial configuration#

\[\nabla\cdot \mathbf F \mathbf S = 0\]

where \(\mathbf F = I + H\) and \(\mathbf S\) is the symmetric stress tensor (Second Piola-Kirchhoff tensor).

Strain measures#

Stress \(\mathbf S\) must be defined as a function of displacement. A common choice is to define the right Cauchy-Green tensor

\[ C = F^T F\]

This has value \(I\) for zero strain. A better formulation uses

\[ E = \frac 1 2 (C - I) = \underbrace{\frac 1 2 (H + H^T + H^T H)}_{\text{stable}}\]

Neo-Hookean model#

Strain energy density \begin{aligned} \psi \left(\mathbf{E} \right) &= \frac{\lambda}{2} \left( \log J \right)^2 - \mu \log J + \frac \mu 2 \left( \operatorname{trace} \mathbf{C} - 3 \right) \ &= \frac{\lambda}{2} \left( \log J \right)^2 - \mu \log J + \mu \operatorname{trace} \mathbf{E}, \end{aligned}

\[\mathbf S = \frac{\partial \psi}{\partial \mathbf E}\]

Stable evaluation#

../_images/nh-initial-stable.svg

Paper on Efficient Methods#

../_images/op_schematic.svg